Obiecte fractale - metode de masurare
Putem identifica:
- un obiect geometric euclidian ( un cerc este locul geometric al unor puncte situate la aceeasi distanta fata de un punct numit centru; în miscarea sa, compasul descrie o urma continua ce aditioneaza, punct dupa punct, pâna la închiderea conturului) si
- un obiect fractal se genereaza printr-un proces recursiv ce impune o anume corelatie la toate scarile obiectului.
Concret, un fractal geometric poate
fi construit pornind de la un mod de divizare a unei linii si repetarea
aceluiasi algoritm de mai multe ori. Altfel spus presupune aplicarea iterativã
a unei legi de generare (generator) asupra unui initiator (starea initiala
- linie, suprafatã, volum) un proces recurent.
Fractalii obtinusi prin constructii matematice se pot împarti în
doua mari categorii:
- fractali obtinuti prin divizare (setul Cantor, curba Koch, curba Peano, covorul Sierpinski); observatie: nu exista o cea mai mica scara;
- fractali obtinuti prin procese de crestere, în care caz se porneste de la un germene ce se dezvoltã prin alipiri succesive ale unor structuri similare germenului (observatie: nu exista o cea mai mare scara)
Curba von Koch - denumita si curba triadica a lui von Koch, 1904, este definita astfel (fig.6): Un segment de dreapta de lungime (L) considerat unitate (initiatorul) se împarte în trei, se îndeparteaza segmentul din mijloc si se înlocuieste cu un triunghi echilateral fara baza
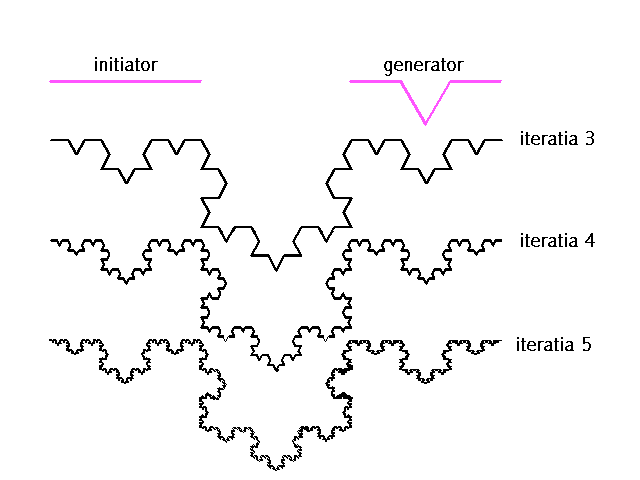
fig. 6
Daca initiatorul este un segment
de dimensiune orizontala L, la iteratia 1 segmentele de baza vor avea
ca lungime s1=L/3, deci curba masurata la scara L/3 va avea un numar de
elemente egal cu patru, N=4 si o lungime egalã cu 4L/3 (N*s). Deci,
relatiile care dau lungimea u a curbei depind de scara ( u=4n*L/3n astfel
rezulta u=4n/3n*L)
La o iteratie anume curba obtinuta nu este un fractal ci, urmând
denumirea lui Mandelbrot, un prefractal. Un fractal este un obiect obtinut
ca limita a unui sir de prefractali când numarul de iteratii n tinde
la infinit. In limbajul curent se face adesea asimilarea între fractali
si prefractali.
Reprezentarea de mai sus este un prim exemplu de lege de scara care reprezinta
o relatie generala existenta între diversele marimi adimensionale
care descriu sistemul, în acest caz fiind vorba de o lege putere.
Numeroase filtre utilizate în biologie, în lucrarile de laborator sau în hemodializa, în operatiile de conditionare industriala a aerului etc. trebuie modelate pentru a putea fi mai usor integrate în sistemele moderne de proiectare asistata de calculator. Majoritatea semifabricatelor si pieselor componente din agregatele, echipamentele sau masinile ealizate pot fi descrise prin teoria elementului finit aplicata unor forme geometrice elementare, nu acelasi lucru se poate spune despre filtre. Distributia si conectivitatea porilor este esentiala pentru a putea caracteriza si modela cu adevarat comportarea unui filtru. Aici, procesul de modelare trebuie sa fie capabil sa surprinda legi de distributie naturala, pe care procesul de evaluare empiricã le dovedeste a fi fractale. Din acest punct de vedere, cele mai simple modelari sunt cele de tip "site ale lui Serpinski". Initiatorul este un triunghi plin, iar prin aplicarea generatorului (împartirea fiecarei laturi a triunghiului în 2 parti egale, deci N=2, unirea mijlocului fiecarei laturi cu mijlocul celeilalte si eliminarea triunghiului astfel format din mijloc) se obtin 3 triunghiuri autosimilare. Prin repetarea la nesfarsit a acestui algoritm se obtine sita lui Sierpinski (fig. 7). Este interesant de observat ca sita Sierpinski combina autosimilaritatea cu o alta simetrie clasica, rotatia. Structura este congruenta cu ea însasi daca se roteste în jurul centrului propriu cu un unghi de 1200 sau un multiplu întreg de 1200. Acest tip de simetrii care combina scari de masura infinite cu rotatii finite, pot fi vazute la multi fractali, în special în desenele lui M.Escher.

fig. 7