Problema anizotropiei si analiza fractala

O variate spatiala sau temporala a unor parametri fizici sau chimici este în masura sa genereze subiectului uman o stare de traire care declanseaza, mai mult sau mai putin constient, un mecanism de evaluare a realitatii, bazat pe o ordonare, clasificare si implicit reconoastere a unei situatii devenita în timp stabila si etichetata corespunzator. O variatie, la modul cel mai general, implica o modificare a unui parametru fizic descriptibil printr-un scalar, vector sau a unui tensor atasat spatiului euclidian 1D,2D,3D. De asemenea, implica accesul la cel putin 2 puncte (în spatiu sau în timp) între care trebuie sa existe o diferenta decelabila . Acea "distanta" minima temporala sau spatiala este dependenta de proprietatile unui corp de proba, a unui captor si a traductorului atasat de a-si putea schimba o proprietate care sa lase în final o anumita "urma" decelabila în planul mental al observatorului. Altfel spus, procesul de perceptie si implicit metodologia de modelare si conceptualizare a oricaror obiecte, fie ele naturale, fie artefact, este strâns legata de interactiunea dintre minte si materie, de modul în care omul reflecta în planul mental realitatea. Rudimentele subtile de spatiu si timp pe care mintea omului le detine înca din primele luni de viata, ordoneaza într-un anume fel specific informatiile legate de variatii ale distantei (trairea sentimentului de spatiu) si ale variatiei temporale (trairea sentimentului de succesiune, de ordonare, de durata -si împreuna- de timp). O evaluare calitativa este deci imprimata înca din momentul în care memoram primele acte de contact cu exteriorul, în primele momente de existenta biologica. Este esential pentru psihologie (dar nu numai) de înteles modul în care functioneaza acea parte neurala, responsabila cu perceptia prin comparatia permanenta cu o scara de semnificatii si sensuri profunde dobândita în trecutul individual sau preexistenta.

Existã undeva profund, în noi însine, o nevoie de ordine, de unde probabil si derivã nevoia abordarii rationale ce implica identificarea unor constante (arhetipuri, rudimente de ordine) într-o lume aflata în continuã miscare (fluctuatie). Putem spune de asemeni ca Lumea nu este asa cum o descriem, cum o "stim", caci ceea ce vedem si cunoastem este rodul unui proces mai complicat, înca neelucidat, de cognitie. Este ca si când mintea cauta permanet sa detaseze din "fondul" de fluctuatii cu care interactioneaza acele aspecte ce devin "forma" si care focalizeaza atentia observatorului din noi, permitând atasarea unor "etichete". Pe un fond omogen, sau foarte dezordonat, un obiect cu o anumita structura se detaseaza si "intra în atentie". Odata focalizata atentia asupra "obiectului" decupat din Realitate apare procesul de cunoastere si apoi de recunoastere calitativã. Poate începe apoi si un alt tip de cunoastere: cea cantitativã. Acest proces presupune tot o comparatie, cea dintre obiect si un etalon- parte omogena cu obiectul masurat. Este esential de înteles ca aceste unitati de masura cu care azi se opereaza, sunt obietiv elaborate si validate de teorii sofisticate ce se sprijina reciproc formând în ansamblul lor paradigma actuala.
Din aceasta perspectiva, demersul stiintific implica o abordare calitativ-cantitativã, bazatã pe o ordonare logica a informatiei culese de la acele clase de obiecte si fenomene care se supun unei reguli de "aur" a stiintei: sunt reproductibile, simple si formalizabile într-o viziune structurala.

Ramâne de vãzut modul în care se va schimba aceastã regulã odatã cu întelegerea procesului cognitiv, cu dezvoltarea tehnicilor de evaluare a sistemelor neliniare, cu integrarea cunostinþelor asupra Complexitãtii etc. O perceptie a unui alt mod de evaluare al starilor si trairilor, structurarea unui spatiu semantic nou, bazat pe o alta alaturare de valori sau chiar pe o alta "împachetare a trairilor" poate avea consecinte esentiale în reformularea paradigmei si implicit în reformularea modului de masurare.

Un prim pas în aceasta directie (este doar o etapa intermediara pentru trazitia la o alta paradigma de masurare si utilizare tehnologica a realitatii) îl presupune abordarea din alta perspectiva a complexitatii. Considerând o directie pe care se manifesta tranzitia de la "simplu" la "complicat" se poate afirma ca notiunea de complex nu se afla undeva pe acea directie fiind de alta calitate. De asemeni, considerând o axa ce permite pozitionarea unei structuri de la o ordine geometrica la o dezordine totala , putem afirma ca o structura complexã nu se va afla undeva pe acea axa, caci este de alta calitate.

In concluzie, paradigma complexitatii ce se formeaza în aceasta perioada încearca sa abordeze, sa conceptualizeze si în final sa utilizeze o alta fateta a Realitatii, mult mai fluctuanta pentru "gustul" omului de stiinta traditional. Punctul de plecare îl constituie o reformulare a conceptului de întâmplare, de anizotropie, o abstractizare a modului de descriere a obiectelor naturale si implicit definirea, delimitarea unor spatii în care sa poate fi identificati "invariantii". La o prima vedere se poate spune ca nu este mare diferenta conceptuala (ajungem tot la invarianti) doar ca invariantii nu mai sunt atasati direct obiectelor sau unor proprietati ale acestora ci naturii variatiilor în timp a acestor proprietãii, determinatã într-un spatiu convenabil ales si topologic echivalent cu fenomenul studiat.

Clasificate pâna nu demult în clasa "zgomotelor" si deci neinteresante din punct de vedere practic, variatiile neperiodice devin azi obiectul principal de studiu. Problema anizotropiei de orice fel constituie azi un punct important de plecare în activitatea de reevaluarea punctelor de vedere privind informatia utila ce poate fi dobândita prin analiza geometrica sau a dinamicii atasate procesului de genezã si evolutiei a numeroaselor fenomene:

-caracterizar ea cantitativa, multiparametrica a aspectelor morfologice ale imaginilor microscopice,
-diagnoza sistemelor artificiale sau naturale,
-în întelegerea mecanicii ruperilor prin urmãrirea propagãrii fronturilor de fisurare,
-modelarea proceselor de solidificare a materialelor urmãrind cu predilectie germinarea si solidificarea dendritica,
-studiul raspunsului unor materiale la diferiti stimuli si sarcini exterioare etc.
Asemenea studii, în general multiparametrice, pot oferi informatii esentiale asupra proprietatilor sistemului investigat, cu atât mai mult cu cât sunt încadrabile în clasa sistemelor complexe. In limitele celor spuse mai sus, pentru moment ne limitam la a verifica pe datele preluate clasic, acele aspecte ce pareau extrem de dezordonate, fara componente periodice si care pot fi acum discriminate si clasificate în structuri fractale, haotice, cu corelatie pe scara larga, auto-similare etc. si verificarea pentru noile clase astfel obtinute a raspunsului pe care acestea îl manifesta fata de anumiti stimuli externi.
Denumirea de neregularitate încearca sa sugereze o esenta comuna a modului în care este azi perceputa realitatea spatio-temporala, atât pentru o fluctuatie ce se manifesta în timp (x(t)) cât si în spatiu (Z(x,y)). O neregularitate poate fi conceputa ca fiind rodul unei întâmplãri, ca produs obtinut în lipsa unor interactiuni capabile sa constrânga si coreleaze pentru a da FORMÃ.

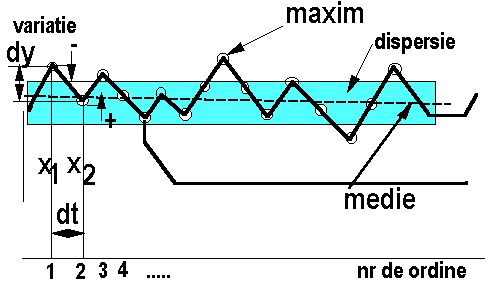
Studiile urmaresc sã evidentieze un alt aspect al "obiectelor" neregulate , cel legat de structura, obiectiv diferit de cel clasic,care, prin chiar natura metodologiei utilizate, conduce la obtinerea de valori medii ce "sterg" structura obietului analizate. Concret, fie o serie temporala definita prin esantioanele ei xs, x2,.., xn. Intre esantione exista un interval constant de timp dt, egal cu timpul de esantionare. Esantionul xieste evaluat cantitativ într-o scara conventionala de valori. In figura 1 se prezinta seria temporala. Constatam câteva caracteristici:

-de la un pas la altul, se identifica sau nu un salt ce poate fi la rândul lui (+) sau (-),
-se poate evalua o marime a saltului (dy)

Si teoriile elaborate sunt diferite, caci pornesc de la obiecte din realitate, ele în sine diferite si folosesc un set de cuvinte si definitii specifice. Si cu toate acestea existã o tratare matematica comunã: medie, dispersie, spectrul Fourier, analiza statistica a duratelor dintre tranzitii, dimensiune fractalã, exponent Lzapunov, Hurst etc. S-a dorit astfel a se preciza ca exista asemanari si deosebiri esentiale atunci când acordam semnificatie unei variatii si cã variatia în sine, caracterizatã prin metode specifice, are o serie de proprietati ce pot fi ulterior asociate cu fenomenul studiat. De aceea vom reveni la exemplul din figura 1 ce sugereaza grafic perspectiva din care se priveste în continuare analiza seriilor temporale. Un prim pas de abstractizare îl constituie faptul ca digitizarea (conversia numerica) face ca fenomenul analizat sa "înghete" într-o succesiune de numere întregi, functie de capacitatea sistemului de achizitie de a decela un semnal analogic (2n biti, uzual n este cuprins între 8 si 24). Se analizeaza în continuare un sir de numere. Sa încercam sa vedem acum acest sir de numere ca fiind succesiunea profilului unei chei (figura 2).

Putem identifica astfel doua perspective:

clasa I- masa partii active a cheii, gradul de regularitate sau neregularitate al "zimtilor" caracterizat prin: înaltimea medie a acestora, dinamica maxima, dispersia, etc...
clasa II- ordinea zimtilor (pattern), ordine ce determina exclusiv functia de "deschidere" selectiva a usii.

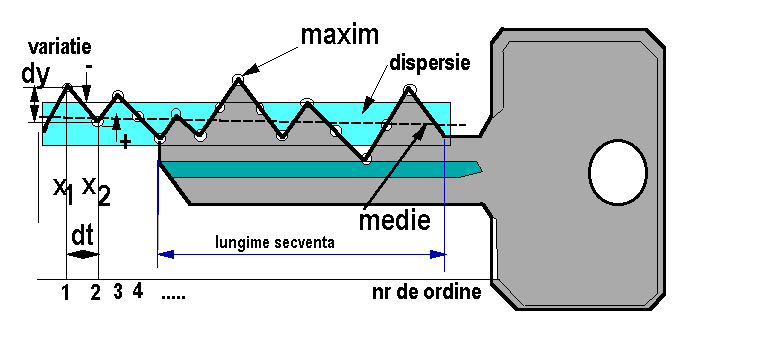
fig. 2

Se poate întelege imediat cã o reorganizare a acelorasi valori într-o alta succesiune lasa nemodificat orice parametru din clasa I, dar face cheia complet inutilizabila pentru operatia pentru care a fost conceputa: deschiderea usii.

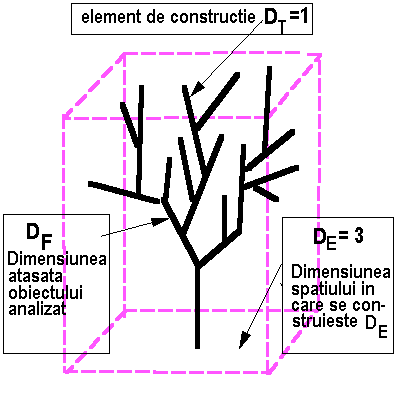
In general, obiectele sunt descriptibile într-un spatiu euclidian tridimensional. In cazul unor corpuri geometrice ideale, structura compacta a obiectului face ca dimensiunea sa sa corespunda cu dimensiunea spatiului în care este acesta scufundat. Pentru a fi mai explicita ideea de neregurlaritate a unui obiect real si implicit sensul demersului nostru în continuare, sa consideram o structura arborescenta tridimensionala (figura 3), de tipul unui arbore, realizata dintr-un element ideal de constructie uni-dimensional (deci dimensiunea topologica a elementului de constructie este 1).

Putem concluziona prin acest experiment filozofic ca evaluarea neregularitatii spatiale urmareste de data aceasta, nu aspecte statistice, în medie adevarate, ci estimarea cantitativa a sructurii si texturii unui obiect ce prezinta discontinuitati.
Imaginea de mai jos încearca sa sugereze diferenta majora dintre cele doua atitudini de evaluare cantitativa a unor structuri neregulate, precum cea din figura 4 (electrodepunere de Cu).

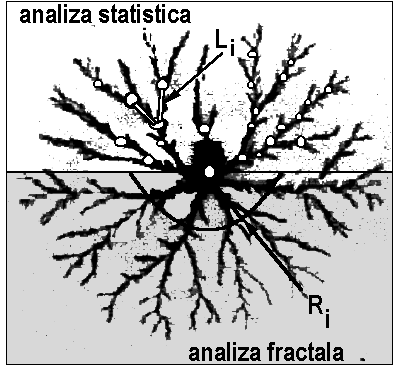
fig. 4

Analiza statistica presupune o "spargere" a unitatii obiectului în elemente "constituente", masurarea lor cantitativa si elaborarea unei metodologii de sinteza a rezultatelor astfel obtinute (media Li, dispersia Li sau chiar functii cum ar fi functia de repartitie sau de distributie). Analiza fractala, de exemplu, masoara obiectul în unitatea sa. In cazul sugerat ce va fi analizat concret în continuare se urmareste determinarea unui exponent D dintr-o masurare de forma Li(ri) ~ ri D unde ri este raza în interiorul careia se calculeaza lungimea totala Li. Acest exponent, intervalul minim si maxim al razei ri pentru care relatia de tip putere este valabila se va adauga la informatia statistica obtinuta clasic, permitând astfel o mai buna caracterizare a unei imagini ce parea dezordonata.

Este deci de observat de la început ca procesul de masura urmareste altceva (evaluarea cantitativa a structurii ) si se realizeaza într-un mod specific: prin masuratori multiple, la scari (rezolutii) diferite, cautându-se diferite corelatii între aproximatele succesive astfel determinate.

Fractali • Obiecte fractale • Dimensiunea fractala • Covorul lui Sierpinski • Proiectant