Este o alta forma de repartizare a unor goluri pentru a modela o "sita naturala". In acest caz, factorul de scara este 3, adica initiatorul constituit dintr-un patrat plin este divizat în 9 parti egale din care se îndeparteaza partea centrala. Raportul de masa este 8, adica sunt 8 patrate negre ramase prin eliminarea celui din mijloc (fig.1).

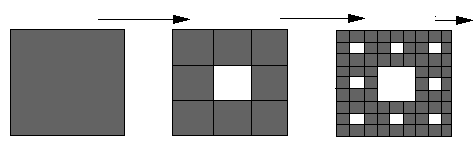
fig. 1

Numarul de obiecte geometrice generate recurent este extrem de mare. Amintim doar ca exista doua categorii esentiale ce asigura o apropiere de realitate a obiectelor generate si apoi utilizate în a descoperi proprietati noi ce decurg din înlocuirea conceptului de mediu omogen si izotrop din modelele clasice de comportare a materiei în diferite câmpuri fizice si chimice cu un mediu anizotrop structurat fractal, mai aproape de realitatea fizica.
Exista asa numitii: fractali neuniformi si fractali aleatori. Fractalii neuniformi iau nastere prin aplicarea simultana a 2 factori de scara, (fig.2).

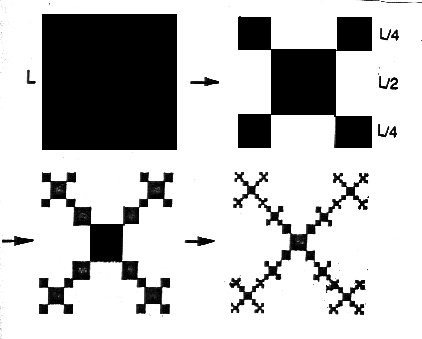
fig. 2.

Aceasta structura este mai complicata si intra în categoria multifractalilor. Fractalii aleatorii sunt fractalii a caror lege de constructie nu asculta de legi deterministe. Astfel, numarul de obiecte ce se genereaza la fiecare iteratie, precum si pozitia lor este aleatoare. Dimensiunea fractala devine o proprietate a ansamblului statistic de obiecte.
Una dintre primele functii fractale aleatoare studiate a fost traiectoria miscarii browniene. Dimensiunea fractala a graficului deplasarii unei particule browniene în timp este 1,5. Aceste structuri prezintã un interes deosebit în modelarea si investigarea structurilor reale.

Probabil cel mai cunoscut fractal al tuturor timpurilor este asa-numitul triunghi al lui Sierpinski. Modul de realizare al acestui fractal este foarte simplu: la inceput se deseneaz„ un triunghi pe care il vom diviza in patru parti egale, iar trei dintre ele (cele din exterior) vor fi s i ele divizate (folosind acelasi procedeu), procesul continuand la infinit pentru toate triunghiurile formate. In figura de mai jos este prezentata modalitatea de constructie descrisa anterior.

fig. 3 Triunghiul lui Sierpinski

Desigur, pentru a putea realiza forma matematica imaginata de Sierpinski ar insemna sa putem trasa linii de divizare infinit de mici. In figura sunt ilustrati doar primii pasi efectuati.

O alta modalitate de realizare a acestui fractal este urmatoarea: se porneste de la un triunghi plin in care se decupeaza triunghiuri egale cu un sfert din triunghiul initial. Daca repetam la infinit acest proces, atunci vom obtine un fractal identic cu triunghiul lui Sierpinski (uneori, cand este realizat prin aceasta tehnica el se mai numeste si garnitura lui Sierpinski. Primii pasi ai acestui procedeu sunt prezentati in figura 4.

fig. 4 Garnitura lui Sierpinski

Pana acum totul ar parea in regula, nici o lege a matematicii nefiind incalcata. Problema a aparut atunci cand Sierpinski a incercat sa determine aria pe care o ocupa acest fractal. Pe de o parte am putea crede ca aria este zero, deoarece un numar infinit de gauri acopera in cele din urma orice suprafata plina din triunghi. Pe de alta parte insa, la un moment dat, indepartam doar un sfert din aria ramasa, lasand mare parte inca acoperita si, deci, oricat de mult am repeta aceasta operatiune, intotdeauna va ramane mai mult decat s-a luat. Deci aria nu ajunge niciodata zero. Acest tip de problema l-a tulburat pe Leibnitz si a ridicat dificultati matematicienilor inca din antichitate. Dar, sa vedem, totusi, cat este aria triunghiului lui Siepinski. Chiar daca intuitia sugereaza ca ea ar fi zero, exista o demonstratie care ne arata ca ea nu poate fi zero. Cu toate acestea, comunitatea matematicienilor a hotarat ca aria sa fie considerata zero, acest lucru datorandu-se in principal imposibilitatii raspunderii la intrebarea: "Daca aria nu este zero, atunci cat este?". Neputand combate acest lucru, Sierpinski si colegii lui au admis ca problema ariei infinit de mici, dar diferita de zero a fost doar "un vis urat".

Fractali • Obiecte fractale • Dimensiunea fractala • Covorul lui Sierpinski • Proiectant